Box 2: Curved Space?

Euclidean Geometry is the great example of how to present ideas in a logical framework that Aristotle would approve of:  you start from intuitive notions that anyone would accept, along with some definitions and then show how further ideas are based on these and can be logically deduced from these initial assumptions.  

 Isaac Newton applied the Euclidean logical model to physics in his magnum opus, the Principia Mathematica.  Colin Pask, in his book Magnificent Principia: Exploring Isaac Newton's Masterpiece pays homage to Euclid and his influence:

Euclid's Elements is the first great mathematics book. It is an enduring masterpiece, going through more editions than any book except the Bible. The development of geometry that it presents remains valid today. There are three reasons for the enormous influence of the Elements. First, it shows us how a subject may be developed on the basis of definitions, axioms, and logical rules for working. Euclid provided a model for use in other fields. Second, it gave us the first systematic approach to a branch of mathematics—geometry in a plane and in three dimensions—as well as certain aspects of number theory.

The third thing Euclid gave us is an accurate and consistent piece of theoretical physics, the first such work, according to Einstein.

In the 17th century, both Spinoza and Newton followed Euclid in his logical mode.

Spinoza applied this model to philosophy, structuring his Ethics in a Euclidean manner as explained by the great 20th century mathematican and philosopher Bertrand Russell in his History of Western Philosophy:

The Ethics is set forth in the style of Euclid, with definitions, axioms, and theorems; everything after the axioms is supposed to be rigorously demonstrated by deductive argument... But it would show a lack of understanding to blame Spinoza for his geometrical method. It was of the essence of his system, ethically as well as metaphysically, to maintain that everything could be demonstrated, and it was therefore essential to produce demonstrations. We cannot accept his method, but that is because we cannot accept his metaphysic. We cannot believe that the interconnections of the parts of the universe are logical, because we hold that scientific laws are to be discovered by observation, not by reasoning alone. But for Spinoza the geometrical method was necessary, and was bound up with the most essential parts of his doctrine.

So the influence of Euclidean Geometry has been enormous, but it is important to remember that Euclid's system was a way of organizing and logically proving geometrical ideas that were already known, and did NOT provide a way of mechanically grinding out new theorems or developing new geometries.  

It now even seems likely that the 18th Century philosopher Immanuel Kant was right to suggest that Euclidean Geometry was in some sense hard-wired into our brains and our way of perceiving space.  This does NOT mean, however, that space is necessarily Euclidean, only that we perceive it in a Euclidean way.  So mathematicians began to wonder if in fact space was Euclidean or rather something else!

One particular postulate or first principle in Euclid's Elements seemed different from the rest.  It was the fifth postulate, also known as the parallel postulate:

If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

Many mathematicians believed that this postulate should be a deduction from the other postulates, but no one was able to provide such a deduction.

So geometry was confined for centuries in the Euclidean box until finally, early in the 19th century, a few mathematicians thought about what would happen if you rejected this postulate and said for example:  

There are no parallel straight lines. Every straight line intersects every other straight line at two points.

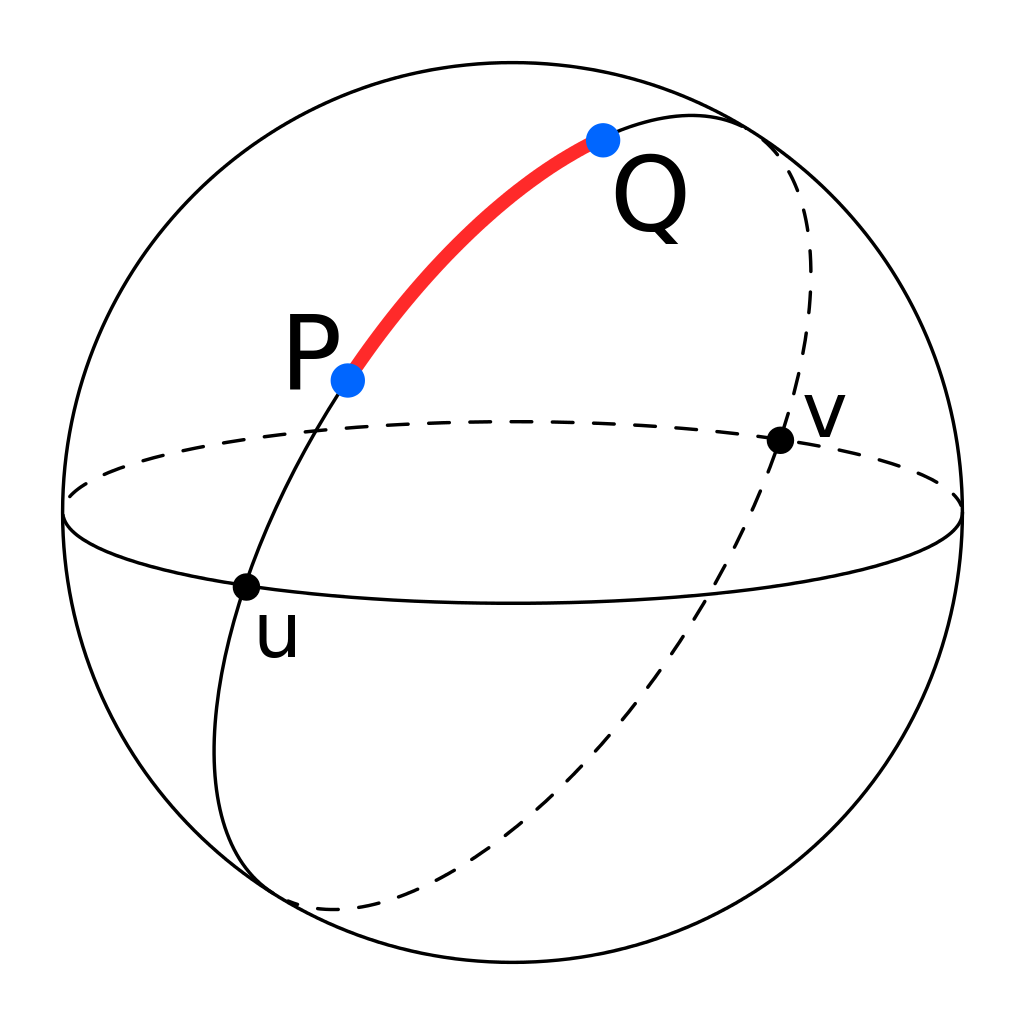
From a Euclidean point of view this sounds like utter nonsense, but in fact it is the basis of spherical geometry or the geometry of our planet's surface!  If we define a straight line as the shortest distance between two points, then on the surface of a sphere or on the surface of the Earth, "straight lines" are in fact "great circles" like the equator that are on a plane with the center of the Earth and always intersect each other:

 Spherical geometry explains why it is actually a shorter route for a jet to swing north when flying from North America to Europe.  On a flat map this would be a longer route, but on a globe it is actually the shorter route!

This means that the shortest path between Los Angeles and London on Earth’s map is not a straight line (red), but rather a curve (purple) that follows a line on the sphere that is Earth. Spheres and Such: How do people use Spherical Geometry?

The mind bending thing is to move from the surface of the Earth to a consideration of spherical space!  This is difficult for our Euclidean brains to conceive, but it is something that mathematicians can do by just adding another variable, so instead of spherical geometry of a two dimensional plane such as the surface of the Earth, we consider spherical geometry of three dimensional space and imagine the Universe as finite:  Your spaceship can fly off in one direction and (like someone going around the world) end up where you started from!
 
And so at the beginning of the 19th century, Non-Euclidean Geometry was born.  It was first explored independently by several mathematicians: the Germans Carl Friedrich Gauss and Ferdinand Karl Schweikart , the Hungarian János Bolyai , and the Russian  Nikolai Ivanovich Lobachevsky

Bernhard Riemann developed his Non-Euclidean Riemann Geometry that led in turn to the study of curved space and the development of tools such as the tensor calculus which Einstein used in his Theory of General Relativity to present gravitation geometrically as a bending of space rather than as Newtonian action at a distance.

 Some entertaining videos on Non-Euclidean Geometry: