Box 10: Heat Wave

 In 1822, the French mathematician Joseph Fourier published his book  Théorie Analytique de la Chaleur (The Analytical Theory of Heat) in which he made use of a bold conjecture that all complex waves can be broken down into simple sine waves:

from Math Is Fun:  Fourier Series

The great 19th Century British scientist William Thomson, Lord Kelvin praised Fourier's book as a "mathematical poem" and paid tribute to it's lasting influence in his Treatise on Natural Philosophy:

The Vibrating String Controversy

Since the time of Pythagoras and the ancient Greeks, mathematicians and scientists have been fascinated with the vibrating string, such as that of a plucked instrument like the harp.  In the 18th century interest in the mathematics of waves increased with the advent of powerful new tools developed from calculus.  

The vibrating string was the elemental problem in wave theory, and by the end of the 18th century it had drawn in many of the greatest names in mathematics, all pitted against one another, each taking a different approach to the problem.

The Language of Physics by Elizabeth Garber offers fascinating insights into what lay behind the mathematical thinking of this era.

It seemed that the vast mathematical powers of analysis that calculus had unleashed made it seem that mathematicians could proceed deductively, in the light of reason alone and without need for scientific experimentation.

And in their ultimate arrogance, great mathematicians like Lagrange believed that the physical science would be absorbed into mathematics:

Lagrange had approached closer than anyone to Fourier Analysis and had even employed it in a few isolated cases, but believed that the mathematics involved was insufficient to yield a general result.  Stronger mathematical tools were needed, he believed and so, by the weight of his reputation, discouraged any further progress in this area, until Fourier arrived on the scene.

Fourier took a different approach, made his bold conjecture and showed time after time that the mathematical results were in accord with the results of experiment.

Mathematicians were dubious at first about Fourier's conjecture but eventually the German mathematician Peter Dirichlet was able to establish Fourier's result as a theorem instead of just a conjecture, and great mathematicians such as Henri Poincare began to sing Fourier's praises:

In the animation below we see sine waves assemble to approach closer and closer to the form of a square wave.

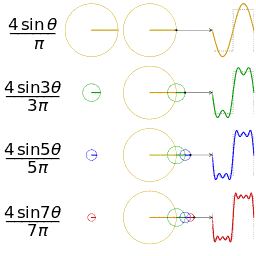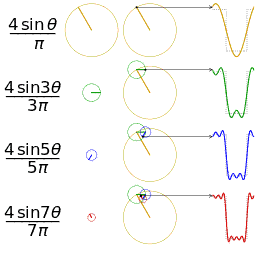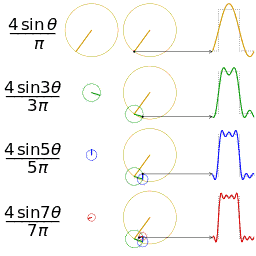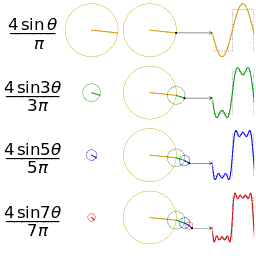From Wikipedia article:  Fourier Series

And here is a video showing this assembly of sine waves:

Likewise, in the animation below we see sine waves assemble to approach closer and closer to the form of a saw-tooth wave.

From Wikipedia article:  Fourier Series

These wonderful animations were developed by Pierre Guilleminot and can be experimented with at his website: 

Fourier series visualisation

There are some excellent and entertaining videos on the background to these animations and Fourier Series in general:

But what is a Fourier series? From heat flow to circle drawings

 

But what is the Fourier Transform? A visual introduction

 

The following video explains what the Fourier series does, and why it is one of the most surprising results in mathematics:
 

The Fourier transform lets you have your cake and understand it

Box 9: Cadmus and Harmonia

Algebra and Geometry had developed and flourished largely apart from one another.  Today we have grown so used to their marriage that it is difficult to realize what a huge step it was getting these two together, a huge step taken independently by two 17th century French mathematical giants Descartes and Fermat:  the development of co-ordinate or analytical geometry.  

Mini Biography - Rene Descartes

Pierre de Fermat: Biography of a Great Thinker

These two mathematicians came at this development from two opposite perspectives:  Fermat started with an algebraic equation and then described the geometric figure that you get from it.  Descartes started with the geometric figure and showed how its properties could be described by an algebraic equation.

Many streams of thought flowed in together to lead to this development.  Omar Khayyam, the great Persian mathematician developed a geometric approach to solving the general cubic equation (the algebraic equation where x is raised to the third power).  Musical notation is essentially a graph of pitch and time.

Fermat & Descartes: Origins of Coordinate Geometry Part 1

Fermat & Descartes: Origins of Coordinate Geometry Part 2

 There is an amusing story of how Descartes came up with the idea of the co-ordinate grid for analytic geometry:

From the Math Education Page:  Cartesian Coordinate Objectives

How Descartes Created the Coordinate Plane

The conic sections studied by the ancient Greeks all have their graph equations:

Try these equations in a graphing calculator.  There are many free graphing calculators available online.  Here is an excellent full featured one to try, provided by Desmos.  If you click on "Edit Graph" (in the lower right corner) you can experiment with the ellipse and see the effect of altering various parameters:

Box 8: May As Well Cut Out Group Theory

As Evariste Galois noted above, algebra in the 19th century was in dire need of a major revolution, but like many revolutionaries he found himself facing an endless series of road blocks and block heads, and it was not until many years after his tragic death that his ideas came to be understood, appreciated and applied in a vast number of areas of mathematics and science.

One of the great uses of algebra from ancient times was the solution of polynomial equations.  Increasingly complicated formulae were found for the solution of quadratic, cubic and quartic equations, that is general equations in a single unknown taken to the powers of 2,3, and 4.  But no one was able to solve the general quintic, or the polynomial that took the unknown to the 5th power:

Galois looked at the family of quintics to determine which ones can in fact be solved, and he showed how his procedures could be generalized to explore the solvability of polynomials of any degree.  

Galois achieved this breakthrough by employing a new algebraic structure called a group.  Groups had been explored before in some isolated cases, but Galois was the first to show the true power of group theory.    

Galois: Biography of a Great Thinker

What is a Galois group and how is it used?

What does Galois theory tell us about equations of degree five and higher?

Evariste Galois a documentary

Abstract algebra and group theory seemed too abstruse and rarified to be of any practical value for science, as the great astronomer James Jeans noted:

But it turned out that group theory could be applied to every scientific field that dealt in some way with symmetry, which is pretty much all of science!

The Use of Group Theory in Particle Physics

Researchers are on the trail of a mysterious connection between number theory, algebra and string theory...

Mathematicians Chase Moonshine’s Shadow

The Story of Moonshine, Part I: 

Symmetry, Number theory, and the Monster 

Symmetry, Algebra and the Monster

Box 7: The Doughnut and the Coffee Cup

What happens when you free geometry from measurement and "quantities" such as angles and line segment lengths, and proceed to draw your geometrical diagrams, as it were, on a flexible rubber sheet that can be stretched and distorted to any imaginable degree?  Can anything worthwhile come of this?  And what kind of world do we have if a doughnut and a coffee cup are one and the same?

Business World:  When is a coffee cup a doughnut?

Sometimes problems present themselves where the issue is not the length or angles of line segments or distances between points, but only their relations to one other.  In such cases, the usual geometric techniques cannot be used and will not apply.  A different sort of geometry is required, and it was not until the 18th century that such a geometry began to emerge.

In his solution to the Seven Bridges of Königsberg puzzle, the great Swiss mathematician Leonhard Euler credits Leibniz as the first to consider geometria situs, or the geometry of position.

Leonhard Euler and the Seven Bridges of Königsberg

  In the city of Königsberg there were seven bridges across the river, connecting four different areas of the city.  An age old problem was to find a route where you cross all the bridges, but every bridge once and once only.

MAA: Leonhard Euler's Solution to the Konigsberg Bridge Problem

Geometers and land surveyors might get out their protractors, compasses, rulers, and plumb lines, but these instruments will be of no use and likewise no equation or arithmetic calculation of any level of complexity will make a dint in this problem. 

In a letter to his friend Carl Ehler, the mayor of Danzig, Leonhard Euler explained that this problem was not something a mathematician could solve:

Thus you see, most noble Sir, how this type of solution bears little relationship to mathematics, and I do not understand why you expect a mathematician to produce it, rather than anyone else, for the solution is based on reason alone, and its discovery does not depend on any mathematical principle.                                                                                  

Letter quoted in the excellent article:

Sachs, H., M. Stiebitz, and R. J. Wilson (1988).

 An historical note: Euler’s Königsberg letters. 

 Journal of Graph Theory 12(1), 133–39.

But clearly the problem preyed on Euler's mind until finally he developed a new approach and a whole new area of mathematics:  topology and specifically the field of graph theory which studies not the graphs we are used to, but rather networks of lines and nodes, such as in the diagram below where we see the the Konigsberg Bridge problem translated into a network of lines and nodes containing the essence of the problem:

Maffs is Phun: The Konigsberg Bridge Problem

 How the Königsberg bridge problem changed mathematics 

- Dan Van der Vieren

Graph Theory continues to find new and fascinating applications in a wide variety of the sciences, including this recent development in Quantum Theory:

Hidden bridge between graph theory and quantum experiments uncovered

Box 6: Set for Paradise or Purgatory

Modern Set theory is largely the brain child of the great mathematician George Cantor.  From a simple idea, it seemed that its power knew no bounds.  Some saw it as the solid foundation of all mathematics and a way to demonstrate that mathematics and logic are essential one and the same.

George Cantor did ground breaking but controversial work on the nature of infinity itself.  Up until his time, mathematicians were hoping that they would only have to deal with "potential" infinity such as was as used in the limit concept in calculus.  But Cantor's amazing results opened a world of different kinds of infinity, and paradoxically of different sizes!

Cantor's Infinity Paradox | Set Theory

Cantor's results often seemed paradoxical, but his logic seemed simple and impeccable.

 Set theory was so powerful and elemental that it seemed it could be used freely and completely without any risk of logical error or confusion, but then some paradoxes crept in, deep in the very heart of set theory, that it would be dangerous to ignore, and which eventually expelled many a mathematician from this paradise and plunged them into a purgatory of uncertainty and even madness. 

The great French mathematician Henri Poincare put it this way:

Gottlob Frege was the first to write a monumental work setting mathematics upon a foundation of logic and set theory.  Unfortunately, just as he was completing this work, a young British mathematician and logician named Bertrand Russell wrote to him about a paradox that undermined the very foundations of his work:

 The paradox is now known as Russell's Paradox and has a popular version called the Barber Paradox, but Russell essentially suffered the same experience as Frege of seeing the foundations of his own monumental work Principia Mathematica fall away when Kurt Godel published his paper entitled:

On Formally Undecidable Propositions of Principia Mathematica and Related Systems


Watch a concise and entertaining account of the whole fascinating story and decide for yourself about undecidability:

There is even an entertaining graphic novel that covers this story from Frege to Godel:

Logicomix: An Epic Search for Truth

There is also a fascinating video series on the making of this ground breaking graphic novel:

So in the end mathematics narrowly escaped being identified with logic and now flies strong and free, but without the firm foundation that logic and set theory could have provided.  

Diminic Walliman  has created a wonderful Map of Mathematics and a video to go with it:

And here is a more humorous map of Mathematics:

“Mathematistan” by Martin Kuppe.   This detailed map of the landscape of mathematics was designed by Martin Kuppe

This map first appeared in Martin Kuppe's amusing video on mathematics:

Box 5: Marvels of Modular Math

Number theory is one of the oldest branches of mathematics and in its classic form deals with plain, old integers without worrying about irrational, imaginary, hyperreal or any other exotic type of number.  Even Leopold Kronecker and the Finitists would find no fault with it.  It deals with the properties of numbers using regular operations like addition, subtraction, multiplication and division.

The problem with number theory was that up until the nineteenth century it was essentially a collection of individual or independent results.  A general approach was needed that would include many results from the past, make new discoveries and suggest new avenues of inquiry.

The man who would supply this much needed, general approach was Carl Friedrich Gauss (1777 – 1855).

 In the time of Gauss, number theory was referred to humbly just as arithmetic or sometimes more a little more fulsomely as higher arithmetic.  It was Gauss' favorite area of mathematics:

 And it was in arithmetic that Gauss produced his first and perhaps greatest masterpiece:

Disquisitiones Arithmeticae   

 

 

You can page through or download

The Original Latin Edition of the Disquisitones 

at the Internet Archive 

 In this work, Gauss was able to break arithmetic out of its box by essentially creating a new kind of arithmetic called modular arithmetic dealing with congruences:

 a is congruent to b, modulus n  means simply that a and b have the same remainder when divided by n, or in other words n divides (a - b) without remainder.

Modular arithmetic is sometimes called clock-face arithmetic because you can arrange the numbers from 0 to n like the numbers on a clock and then essentially continue to add numbers in a spiral, round and round showing their congruences.  Here is the spiral for modulus 5:

Module 8:  Basic Number Theory

Modular Arithmetic not only revolutionized number theory but found applications in an amazing variety of areas, as noted in Wikipedia:  

 In theoretical mathematics, modular arithmetic is one of the foundations of number theory, touching on almost every aspect of its study, and it is also used extensively in group theory, ring theory, knot theory, and abstract algebra. In applied mathematics, it is used in computer algebra, cryptography, computer science, chemistry and the visual and musical arts. 

It is taught as the essential, keystone element of the entire field of Discrete Mathematics:

Discrete Math 1:  Modular Arithmetic

Box 4: Imaginary Numbers Save Lives at Sea

Khan Academy:  Introduction to i and imaginary numbers

 

What were known as imaginary numbers (involving the square roots of negative numbers) eventually combined with real numbers (originally so named to distinguish them from the imaginaries) to became more respectably known as complex numbers and now have a wide variety of practical applications in fields as diverse as electronics, communication and quantum mechanics:

 

Yet these numbers began life as interlopers that no one wanted to take seriously in the highly competitive Early Renaissance race to find general ways to solve equations.

In his book Visual Complex Analysis, Tristan Needham provides a good summary of the difficult and unimaginative early years of imaginary numbers:

The mathematician and philosopher René Descartes was apparently the first to refer dismissively to these unusual numbers as "imaginary" in his discussion of equation solving at the end of La Géométrie:

Math With Bad Drawings:  Imagine all the Numbers...

In Visual Complex Analysis, Tristan Needham goes on to diagnose the basic problem with the hesitant handling of imaginary numbers:

Yes, the square root of negative one was a useful but self-contradictory nuisance to mathematicians until they discovered that it was the portal into a whole new dimension of complex numbers.  

The geometric interpretation made some equations involving complex numbers more approachable and less abstruse, such as this one (known as Euler's Identity) from the article  Innovation in Mathematics by Paul R. Halmos (Scientific American - September 1958)

The first three episodes of an excellent 13 part series on imaginary numbers:

Imaginary Numbers Are Real [Part 1: Introduction]

Imaginary Numbers Are Real [Part 2: A Little History]

Imaginary Numbers Are Real [Part 3: Cardan's Problem]

One of the most interesting and important applications of complex numbers was to electromagnetic fields.  Originally, the idea of Action at a Distance was taken as gospel for gravitation and also applied to electricity and magnetism.  Then along came the magnificent experimenter Michael Faraday who came up with the idea of the Electromagnetic Field to fill the void that Action at a Distance left in the space around magnets and electrical apparatus.

While being one of the greatest experimenters of all time, Michael Faraday did not use much mathematics in his theories, and it was left to James Clerk Maxwell to develop the mathematical theory of electromagnetic fields, and the mathematics he brilliantly applied was the theory of functions of a complex variable, or complex analysis.

Both Faraday and Maxwell were two of Einstein's heroes and there is a wonderful book about them and the mathematical development of electromagnetic field theory entitled Einstein's Heroes: