Business World: When is a coffee cup a doughnut?
Sometimes problems present themselves where the issue is not the length or angles of line segments or distances between points, but only their relations to one other. In such cases, the usual geometric techniques cannot be used and will not apply. A different sort of geometry is required, and it was not until the 18th century that such a geometry began to emerge.
In his solution to the Seven Bridges of Königsberg puzzle, the great Swiss mathematician Leonhard Euler credits Leibniz as the first to consider geometria situs, or the geometry of position.
Leonhard Euler and the Seven Bridges of Königsberg
In the city of Königsberg there were seven bridges across the river, connecting four different areas of the city. An age old problem was to find a route where you cross all the bridges, but every bridge once and once only.
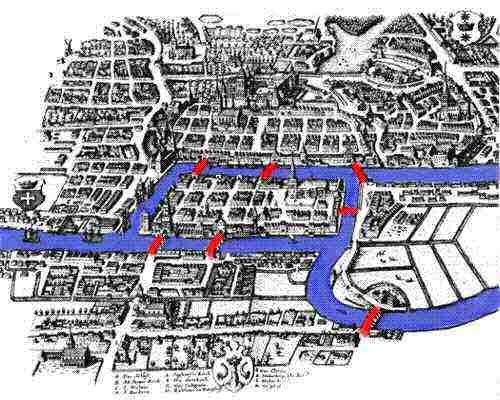 |
| MAA: Leonhard Euler's Solution to the Konigsberg Bridge Problem |
Geometers and land surveyors might get out their protractors, compasses, rulers, and plumb lines, but these instruments will be of no use and likewise no equation or arithmetic calculation of any level of complexity will make a dint in this problem.
In a letter to his friend Carl Ehler, the mayor of Danzig, Leonhard Euler explained that this problem was not something a mathematician could solve:
Thus you see, most noble Sir, how this type of solution bears little relationship to mathematics, and I do not understand why you expect a mathematician to produce it, rather than anyone else, for the solution is based on reason alone, and its discovery does not depend on any mathematical principle.
Letter quoted in the excellent article:
Sachs, H., M. Stiebitz, and R. J. Wilson (1988).
An historical note: Euler’s Königsberg letters.
Journal of Graph Theory 12(1), 133–39.
But clearly the problem preyed on Euler's mind until finally he developed a new approach and a whole new area of mathematics: topology and specifically the field of graph theory which studies not the graphs we are used to, but rather networks of lines and nodes, such as in the diagram below where we see the the Konigsberg Bridge problem translated into a network of lines and nodes containing the essence of the problem:
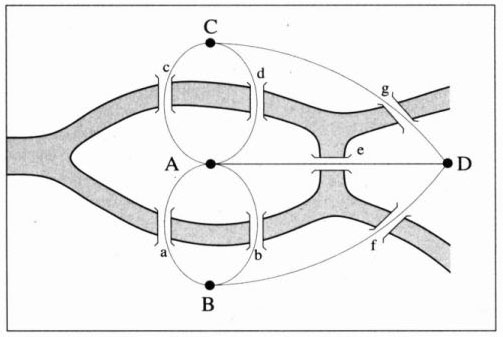 |
|
|









No comments:
Post a Comment
Note: Only a member of this blog may post a comment.